Navigation

Operators and Keywords

Function List:

C++ API

Function File: geom = ls_find_geometry (phi, h = 1, fractol = 1e-3)

Interpret the level-set function phi and extract geometrical properties. A rectangular grid with spacing h uniform in each dimension is assumed. This function assumes the 2D situation.

The function assumes that phi does not contain values which are exact zeros. It is a good idea to use ls_normalise before calling ls_find_geometry. Intersection points with edges very close to a grid point may be pushed away from it, governed by fractol.

The following terms will be used to denote certain elements of the geometrical description returned by this function:

node

A point on the grid. phi is the value of the level-set function at each node. They are numbered from 1 to l x m in the same way as the entries in the matrix phi are numbered.

element

One rectangular cell of the grid. Since we work in 2D, each element is made up of four nodes (which are the vertices of the rectangle). If the grid has l x m nodes, then it contains (l - 1) x (m - 1) elements.

inner element

An element for which each node is inside the described domain.

outer element

An element for which each node is outside of the described domain.

boundary element

An element which has both inside and outside nodes. These elements are intersected by the boundary of the domain and have intersection points on some of their edges.

It can be the case that it has two intersection points (when one boundary edge intersects it) or four (if we have a “narrow pair”). The latter case is that of two intersecting (parallel) boundary edges, which happens when diagonally opposing nodes of the element have the same sign of phi.

A narrow pair is ambiguous as to which intersection points should be connected together. This function is implemented such that it considers the “narrow channel” between the parallel boundary edges to be outside of the domain. In other words, at a narrow pair, the domain is considered to be disconnected instead of connected with a narrow channel.

intersection point

A point on the edge of a boundary element where the boundary of the described domain (approximately) intersects the grid (i. e., phi has a zero). It can be characterised by a pair of inside/outside nodes at each end of the edge it intersects and by the fraction of the side that lies inside the domain.

gamma

The boundary of the described domain. I. e., the curve given by the zero level-set of phi. It may consist of several components, which are each a closed curve.

boundary edge

A single edge of the domain’s boundary, which is a line connecting two intersection points and cutting through a boundary element. It is ordered in such a way that the domain is on the left, if the grid is interpreted as coordinate system. (On the right in matrix ordering.)

The returned variable geom will be a struct with these fields:

dim

The dimension of the grid, equal to size (phi).

elem

Itself a struct describing the elements of the grid. It contains:

n

Number of elements on the grid. Equal to (l - 1) x (m - 1) if phi is l x m.

nodelist

n x 4 matrix containing in its rows the indices of nodes making up each element. According to the ordering in the matrix phi, the nodes are stored in the order SE, SW, NW, NE. Interpreted in a (x, y) grid constructed via meshgrid, the order is instead NE, NW, SW, SE matching the usual numbering of quadrants in the plane. (This is the case because the y axis points down when numbering rows of a matrix, but up in the usual coordinate system.)

type

A vector giving the type of each element. It is -1, 0 and 1 for inner, boundary and outer elements, respectively. (This convention mimics the sign of phi somewhat.)

index

Itself a struct with the fields inner, bdry and outer, containing a list of indices for inner, boundary and outer elements.

These equal the result of find (geom.elem.type == x) with x being -1, 0 and 1.

bdryel

A struct with information about the boundary elements. They have their own index here, which can be mapped to the global element index via geom.elem.index.bdry. Its fields are:

n

Number of boundary elements.

edges

n x 4 matrix, whose columns correspond to the four edges of the boundary elements. For each edge where an intersection point lies, the respective matrix entry is set to the intersection point’s index into geom.ispts. If there is no intersection point, the value is NA.

The edges are ordered similarly to the order in geom.elem.nodelist. In matrix interpretation, the edges are in the columns as S, W, N, E. Interpreted as a coordinate grid, the order is N, W, S, E.

ispts

Struct containing details about the intersection points with the fields:

n

Number of intersection points.

inout

n x 2 matrix containing the node indices of the inner and outer nodes neighbouring each intersection point (in this order).

frac

Fraction of the edge that is inside the domain (connecting the intersection point to the inner neighbour node). This value is always in the range 0–1, independent of h.

incoord

Coordinates of the intersection points relative to the neighbouring inner nodes as a n x 2 matrix. This takes h into account.

onedge

n x 2 x 3 array that indicates on which edges of which boundary elements this intersection point occurs. The first dimension is indexed by intersection point number, the second dimension numbers the (two) boundary elements each intersection point is part of, and the third dimension contains the tuple (boundary element index, edge index, boundary edge index) in the ranges 1–geom.bdryel.n, 1–4 and 1–geom.bedges.n.

The occurances (second dimension) are ordered such that the first one is where the boundary edge “enters” the boundary element, while the second one is where it “leaves” a boundary element.

gammachain

n x 2 matrix that contains for each intersection point the next and previous intersection point indices when following gamma. See also geom.gamma.ispts.

gamma

Struct with information about the components of the domain’s boundary. It contains these fields:

n

Number of gamma components.

ispts

Cell-array with n elements. Each element is a list of indices of intersection points (i. e., indices into geom.ispts). In the order given, they can be joined together to form a closed curve (when also the last one is connected back to the first).

bedges

Information about the boundary edges:

n

Number of boundary edges in total.

comp

A vector giving the gamma component this edge is part of. The components are in the range 1–geom.gamma.n.

ispts

n x 2 matrix containing the intersection point indices that make up each boundary edge.

internal

Data field with additional information for internal use, in particular in ls_build_mesh. The precise format may be subject to change and should not be used.

See also: ls_absolute_geom, ls_normalise, ls_build_mesh, ls_inside.

Demonstration 1

The following code

  n = 15;
  x = linspace (-10, 10, n);
  h = x(2) - x(1);
  [XX, YY] = meshgrid (x, x);

  r1 = sqrt (2) * 2.9;
  r2 = 3;
  phi = ls_union (ls_genbasic (XX, YY, "sphere", [-3, -3], r1), ...
                  ls_genbasic (XX, YY, "sphere", [3, 3], r1), ...
                  ls_genbasic (XX, YY, "sphere", [-5, 5], r2), ...
                  ls_genbasic (XX, YY, "sphere", [5, -5], r2));

  phi = ls_normalise (phi, h);
  g = ls_find_geometry (phi, h, 0.2);
  g = ls_absolute_geom (g, XX, YY);

  figure ();
  hold ("on");

  for i = 1 : size (g.elem.nodelist, 1)
    nodes = g.elem.nodelist(i, :);
    switch (g.elem.type(i))
      case -1
        colour = [0.5, 0.5, 1];
      case 0
        colour = [1, 0.5, 0.5];
      case 1
        colour = [0.8, 0.8, 0.8];
    endswitch
    patch (XX(nodes), YY(nodes), colour);
  endfor

  plot (g.ispts.coord(:, 1), g.ispts.coord(:, 2), "k.", "MarkerSize", 8);
  for i = 1 : g.gamma.n
    pts = g.gamma.ispts{i};
    pts(end + 1) = pts(1);
    plot (g.ispts.coord(pts, 1), g.ispts.coord(pts, 2), "k-", "LineWidth", 2);
  endfor

  contour (XX, YY, phi, [0, 0], "g");

  axis ([min(x), max(x), min(x), max(x)]);
  axis ("equal");
  grid ("on");
  set (gca (), "xtick", x, "ytick", x, "xticklabel", "", "yticklabel", "");
  hold ("off");

Produces the following figure

Figure 1

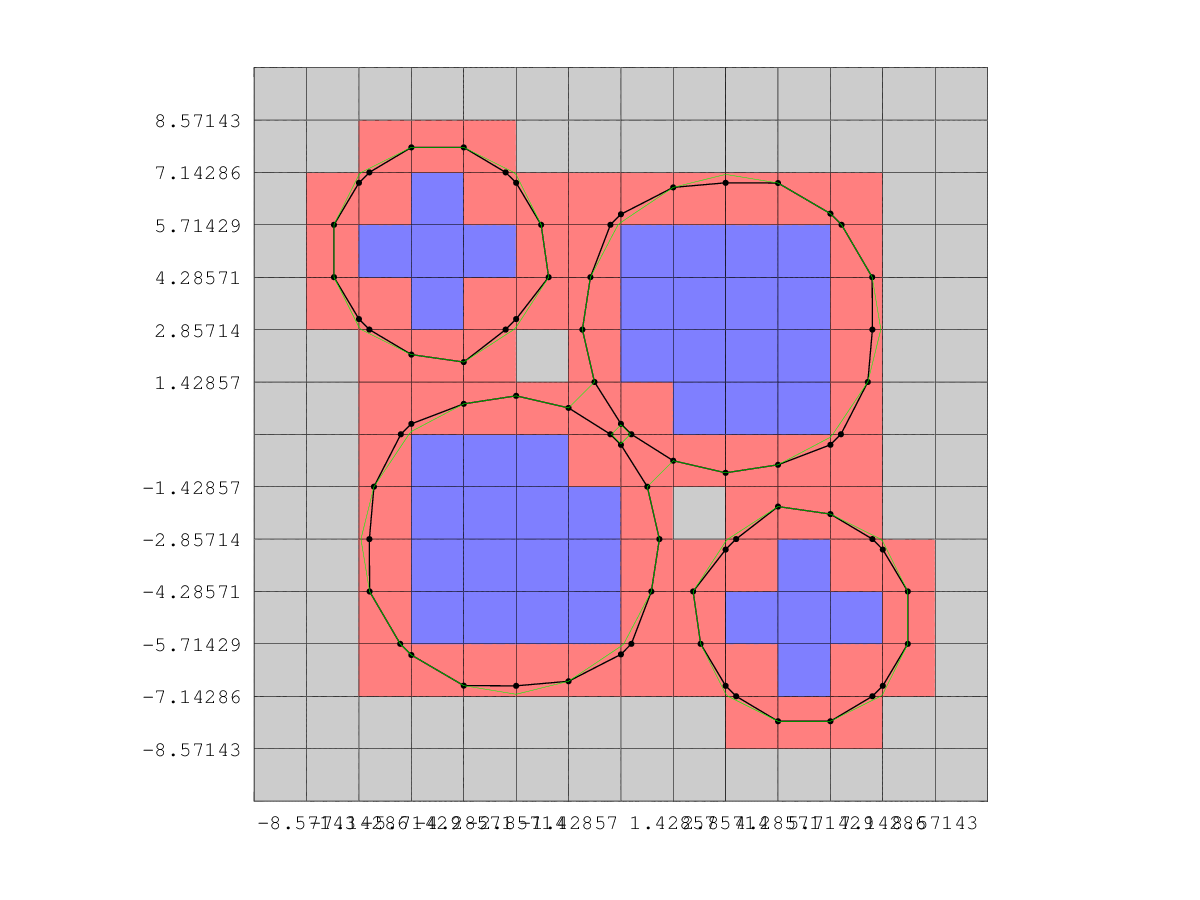Package: level-set