Navigation

Operators and Keywords

Function List:

C++ API

Function File: d = ls_nb_from_geom (geom, phi)
Function File: [d, g] = ls_nb_from_geom (geom, phi, g0)

Initialise the narrow-band values utilising information about the geometry. geom should be the geometry according to ls_find_geometry, and it must contain absolute coordinates as per ls_absolute_geom in addition. Thus it is unnecessary to pass the grid spacing, as this information is already contained in the absolute coordinates. This is an alternative routine to the standard ls_init_narrowband for 2D situations.

This function sets the distance at each node of a boundary element to the shortest distance to any boundary edge according to the geometry information in geom. In contrast to ls_init_narrowband, this also initialises values on the “far diagonally away” point. This makes the result more accurate.

In the second form, g0 is expected to contain the values of some function defined on each boundary edge (ordered in the same way as geom.bedges). These function values will be extended onto narrow-band points as well, and returned in g.

See also: ls_init_narrowband, ls_find_geometry, ls_absolute_geom, ls_solve_stationary, fastmarching.

Demonstration 1

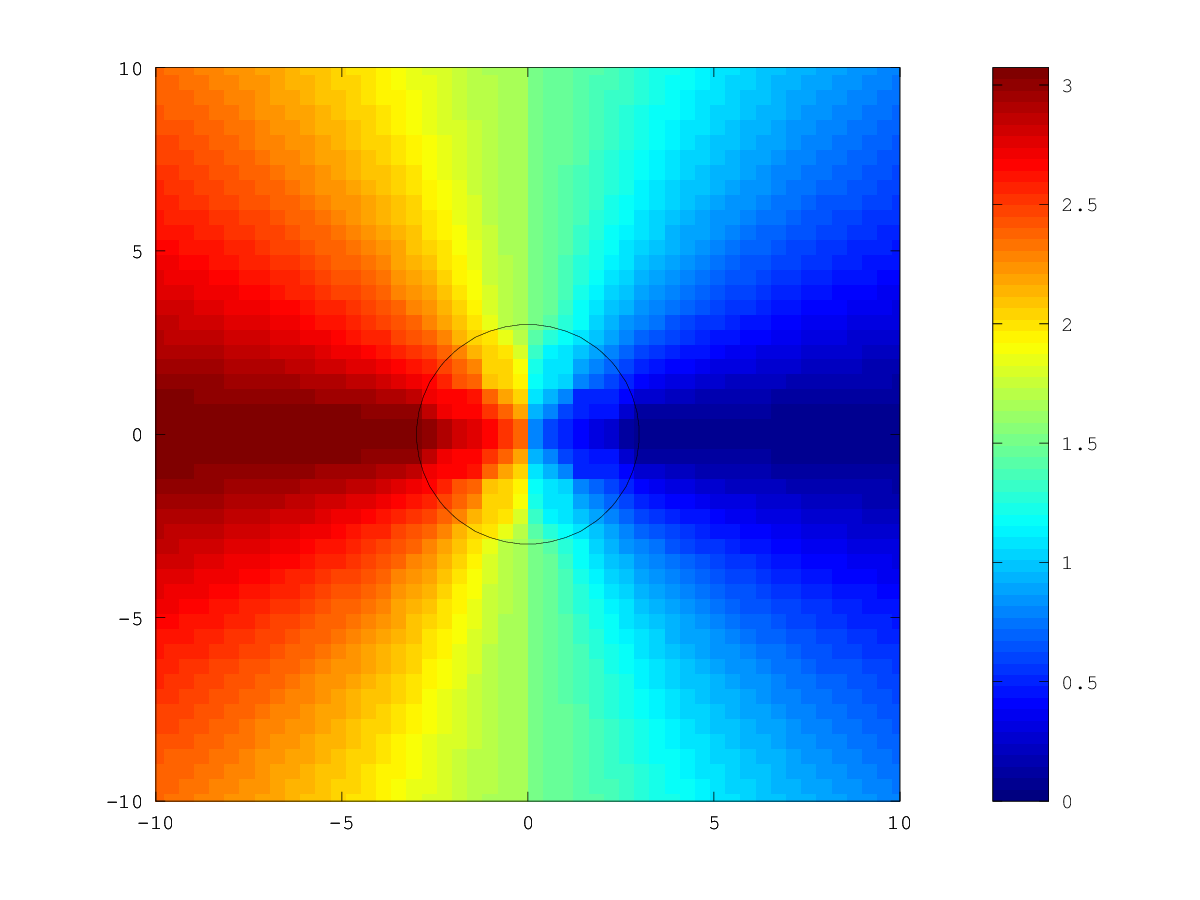
The following code

  n = 50;
  x = linspace (-10, 10, n);
  h = x(2) - x(1);
  [XX, YY] = meshgrid (x, x);

  phi = ls_genbasic (XX, YY, "sphere", [0, 0], 3);
  phi = ls_normalise (phi, h);
  geom = ls_find_geometry (phi, h);
  geom = ls_absolute_geom (geom, XX, YY);

  g0 = NA (1, geom.bedges.n);
  for i = 1 : geom.bedges.n
    a = geom.ispts.coord(geom.bedges.ispts(i, 1), :);
    b = geom.ispts.coord(geom.bedges.ispts(i, 2), :);
    m = (a + b) / 2;
    angle = abs (atan2 (m(2), m(1)));
    g0(i) = min (angle, 2 * pi - angle);
  endfor

  [d, g] = ls_nb_from_geom (geom, phi, g0);
  [d, g] = fastmarching (d, g, h * ones (size (phi)));

  figure ();
  hold ("on");
  imagesc (x, x, g);
  set (gca (), "ydir", "normal");
  contour (XX, YY, phi, [0, 0], "k");
  hold ("off");
  colorbar ();

Produces the following figure

Figure 1

Package: level-set