Navigation

Operators and Keywords

Function List:

C++ API

Function File: d = ls_solve_stationary (phi, f, h = 1)
Function File: d = ls_solve_stationary (phi, f, h = 1, nb)

Solve a generalised Eikonal equation with speeds of arbitrary signs. The equation solved is 

f |grad d |= 1

with d = 0 on the boundary. The domain is described by the level-set function phi on a rectangular grid. f should contain the values of the speed field on the grid points. h can be given as the grid spacing. In the second form, where the optional nb is given, it is used to initialise the narrow band with a manual calculation. By default, the result of ls_init_narrowband is used. Values which are not fixed by the narrow band should be set to NA.

Note that in comparison to fastmarching, the speed need not be positive. It is the reciprocal of f in fastmarching.

This is a preparation step, and afterwards, the evolved geometry according to the level-set equation 

d/dt phi + f |grad phi |= 0

can be extracted from d at arbitrary positive times using the supplemental function ls_extract_solution.

At points where f is exactly zero, the output will be set to NA. This case is handled separately in ls_extract_solution. In the narrow band, the returned distances may actually be negative even for positive f and vice-versa. This helps to avoid unnecessary errors introduced into the level-set function due to a finite grid-size when the time step is chosen small.

See also: ls_extract_solution, ls_signed_distance, ls_nb_from_geom.

Demonstration 1

The following code

  n = 100;
  x = linspace (-10, 10, n);
  h = x(2) - x(1);
  [XX, YY] = meshgrid (x, x);

  phi0 = YY - XX + 15;
  f = sign (XX) + 2;

  d = ls_solve_stationary (phi0, f, h);
  figure ();
  contour (XX, YY, d);
  line ([0, 0], [-10, 10]);
  title ("Refraction");

Produces the following figure

Figure 1

Demonstration 2

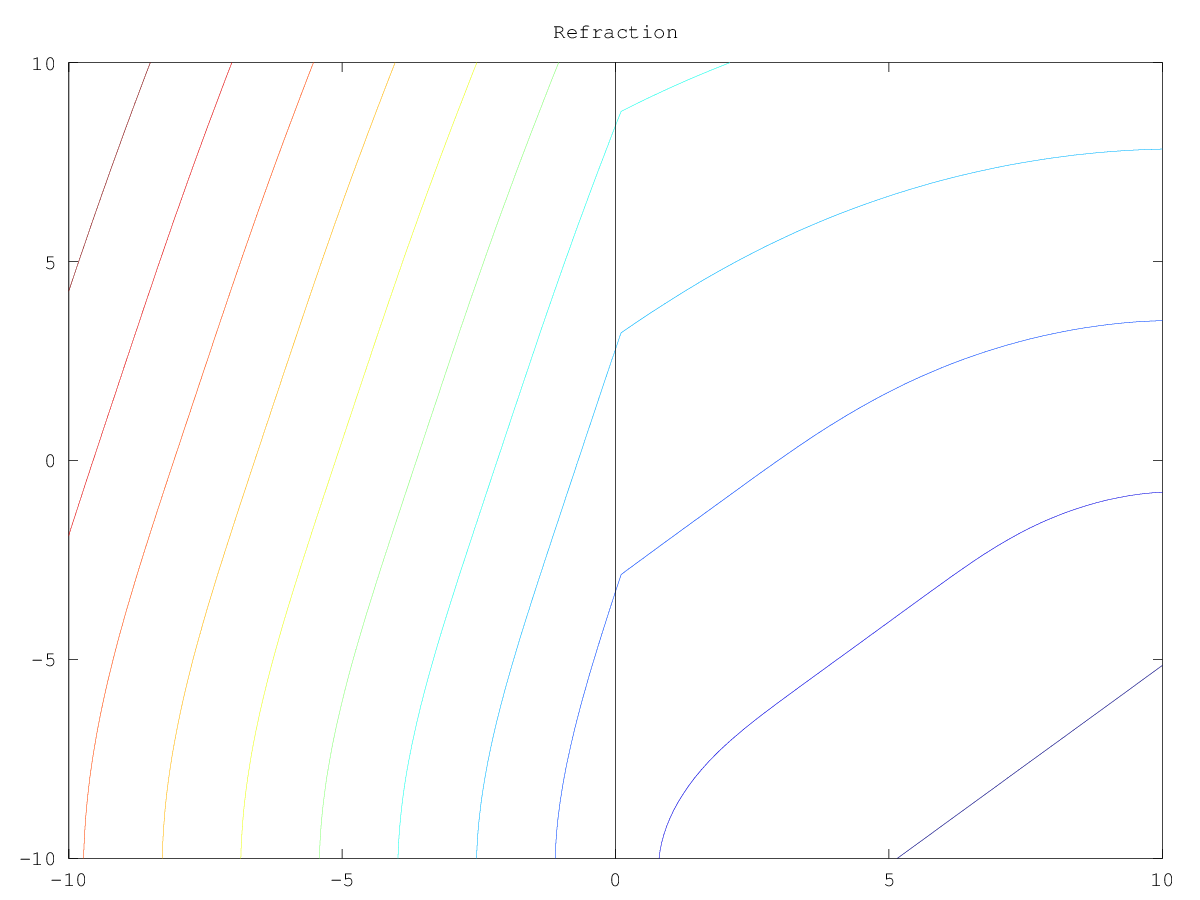The following code

  n = 101;
  x = linspace (-10, 10, n);
  h = x(2) - x(1);
  [XX, YY] = meshgrid (x, x);

  phi0 = XX + 9;
  f = ones (size (phi0));
  f(XX == 0 & abs (YY) > 2) = 0;

  d = ls_solve_stationary (phi0, f, h);
  figure ();
  contour (XX, YY, d);
  line ([0, 0], [-10, -2]);
  line ([0, 0], [2, 10]);
  title ("Diffraction");

Produces the following figure

Figure 1

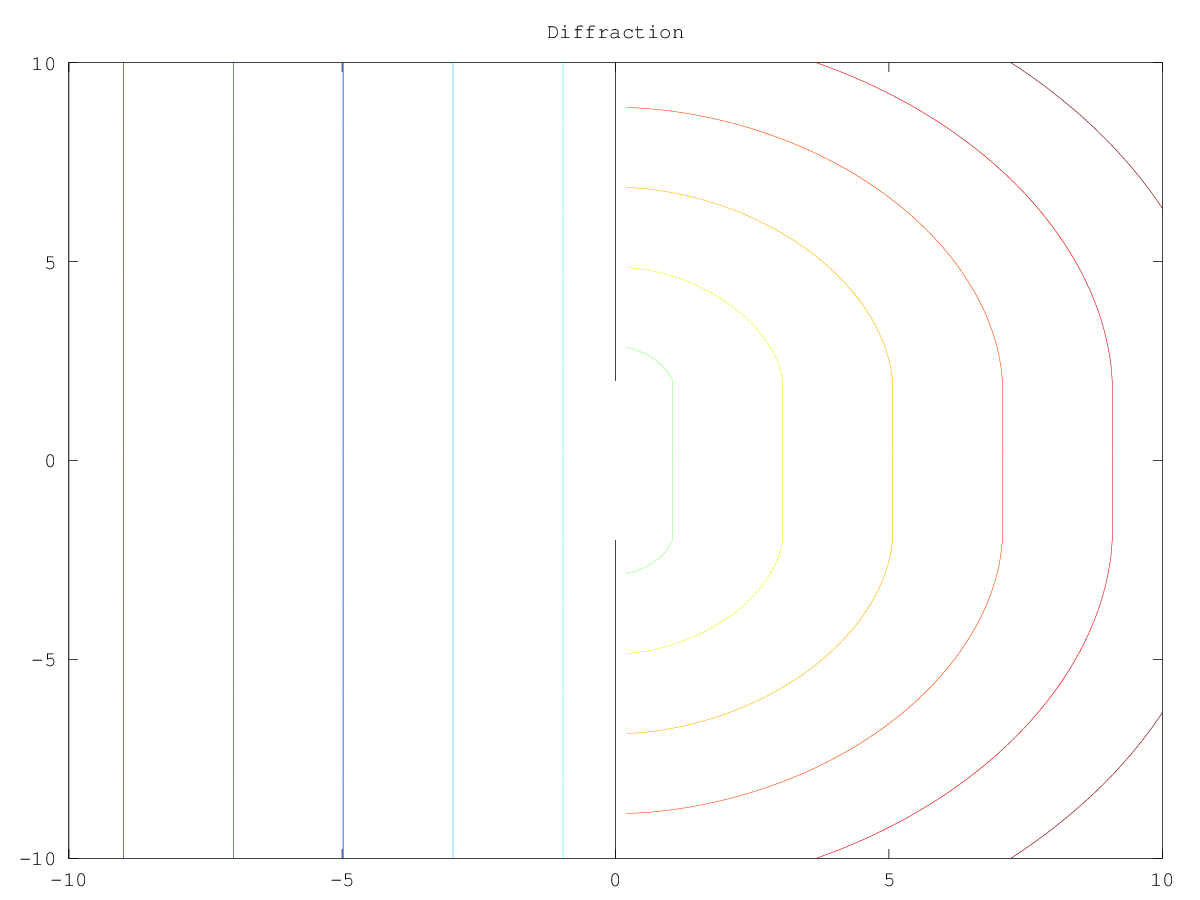Package: level-set