Navigation

Operators and Keywords

Function List:

C++ API

Function File: phit = ls_time_step (t, phi0, f, h = 1)
Function File: phit = ls_time_step (t, c, phi0, f, h = 1)

Evolve the level-set equation with time stepping. Perform explicit time stepping on the equation 

d/dt phi + f |grad phi |= 0.

The initial value is given by phi0. phi0 and f must be of the same size. If h is present, it sets the spatial grid size. The time stepping uses upwind_gradient_norm for the evaluation of the gradient norm at each step.

t is the time (or vector of times) at which the solution should be returned. If more than one time is given, the result phit will be a cell array of the evolved level-set functions at each of the requested time points. If t is a scalar, phit is returned as array of the same size of phi0.

The time step is chosen to satisfy the Courant-Friedrichs-Lewy condition 

dt = c h / (Fm * n).

Here, Fm is the maximum absolute value in f, and n is the number of space dimensions. The desired ratio c is by default one, but can be passed explicitly with the second usage form.

See also: ls_extract_solution, upwind_gradient_norm.

Demonstration 1

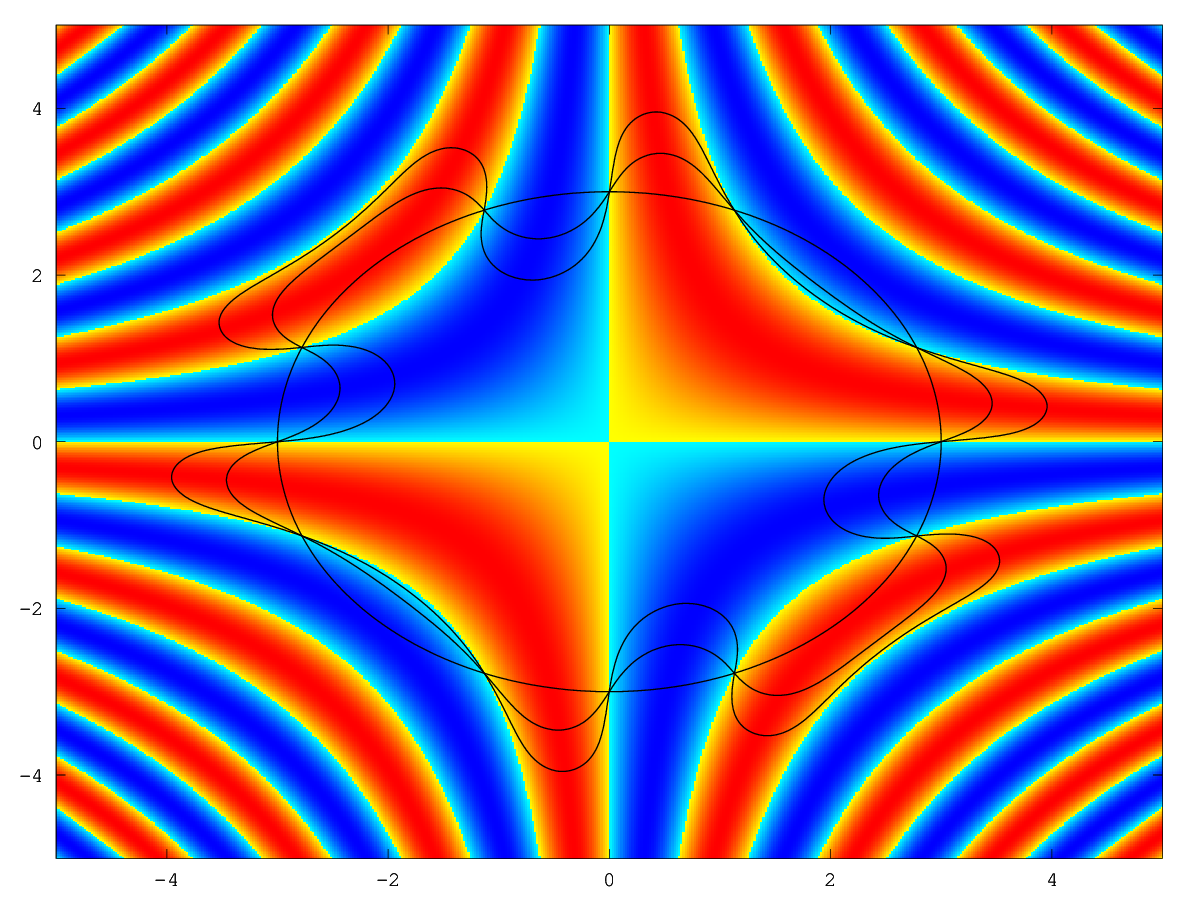
The following code

  n = 500;
  x = linspace (-5, 5, n);
  h = x(2) - x(1);
  [XX, YY] = meshgrid (x, x);

  F = sin (XX .* YY);
  phi0 = ls_genbasic (XX, YY, "sphere", [0, 0], 3);
  phit = ls_time_step ([0.5, 1], phi0, F, h);

  figure ();
  hold ("on");
  imagesc (x, x, F);
  set (gca (), "ydir", "normal");
  ls_sign_colourmap ();
  contour (XX, YY, phi0, [0, 0], "k", "LineWidth", 2);
  contour (XX, YY, phit{1}, [0, 0], "k", "LineWidth", 2);
  contour (XX, YY, phit{2}, [0, 0], "k", "LineWidth", 2);
  hold ("off");

Produces the following figure

Figure 1

Package: level-set