Navigation

Operators and Keywords

Function List:

C++ API

: [t, y] = ode45 (fun, trange, init)
: [t, y] = ode45 (fun, trange, init, ode_opt)
: [t, y, te, ye, ie] = ode45 (…)
: solution = ode45 (…)

Solve a set of non-stiff Ordinary Differential Equations (non-stiff ODEs) with the well known explicit Dormand-Prince method of order 4.

fun is a function handle, inline function, or string containing the name of the function that defines the ODE: y' = f(t,y). The function must accept two inputs where the first is time t and the second is a column vector of unknowns y.

trange specifies the time interval over which the ODE will be evaluated. Typically, it is a two-element vector specifying the initial and final times ([tinit, tfinal]). If there are more than two elements then the solution will also be evaluated at these intermediate time instances.

By default, ode45 uses an adaptive timestep with the integrate_adaptive algorithm. The tolerance for the timestep computation may be changed by using the options "RelTol" and "AbsTol".

init contains the initial value for the unknowns. If it is a row vector then the solution y will be a matrix in which each column is the solution for the corresponding initial value in init.

The optional fourth argument ode_opt specifies non-default options to the ODE solver. It is a structure generated by odeset.

The function typically returns two outputs. Variable t is a column vector and contains the times where the solution was found. The output y is a matrix in which each column refers to a different unknown of the problem and each row corresponds to a time in t.

The output can also be returned as a structure solution which has a field x containing a row vector of times where the solution was evaluated and a field y containing the solution matrix such that each column corresponds to a time in x. Use fieldnames (solution) to see the other fields and additional information returned.

If using the "Events" option then three additional outputs may be returned. te holds the time when an Event function returned a zero. ye holds the value of the solution at time te. ie contains an index indicating which Event function was triggered in the case of multiple Event functions.

Example: Solve the Van der Pol equation 

fvdp = @(t,y) [y(2); (1 - y(1)^2) * y(2) - y(1)];
[t,y] = ode45 (fvdp, [0, 20], [2, 0]);

See also: odeset, odeget, ode23.

Demonstration 1

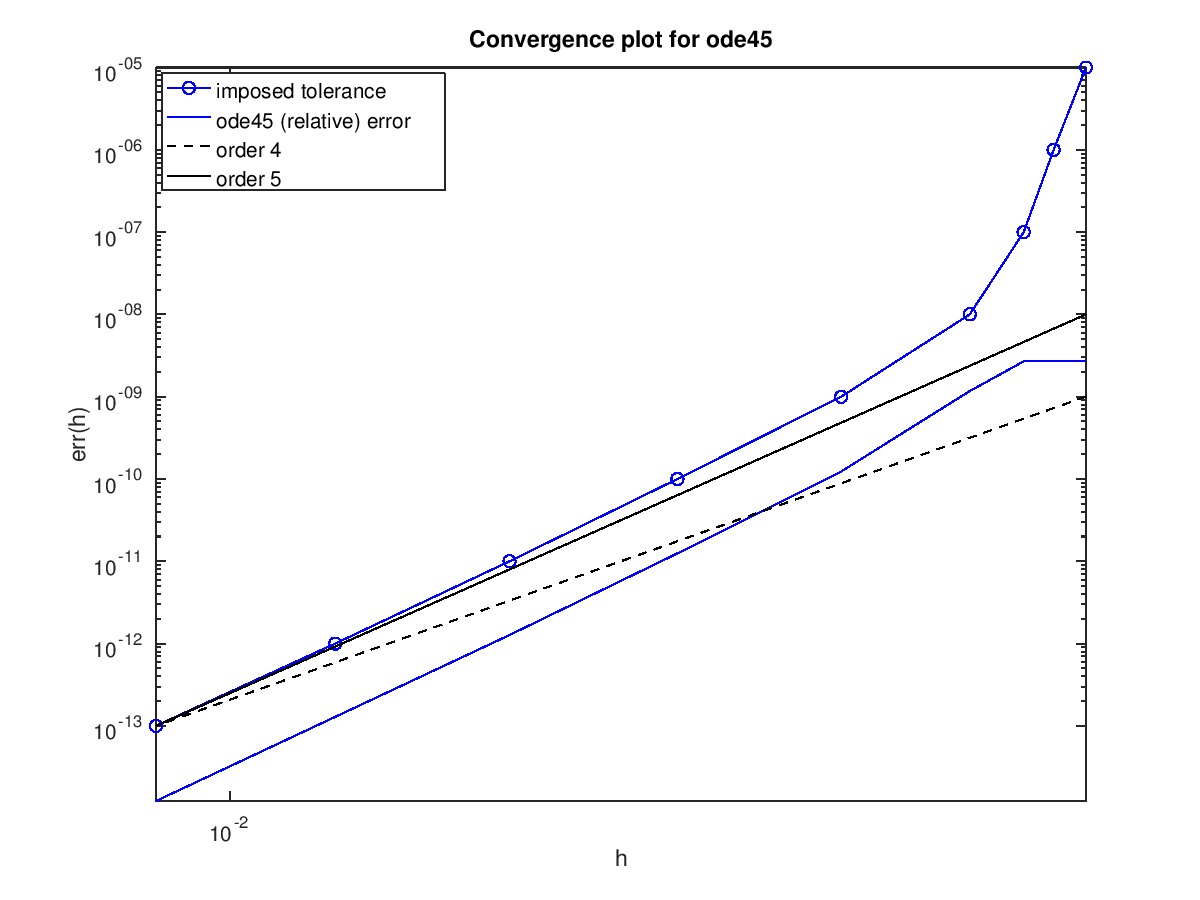
The following code

 ## Demonstrate convergence order for ode45
 tol = 1e-5 ./ 10.^[0:8];
 for i = 1 : numel (tol)
   opt = odeset ("RelTol", tol(i), "AbsTol", realmin);
   [t, y] = ode45 (@(t, y) -y, [0, 1], 1, opt);
   h(i) = 1 / (numel (t) - 1);
   err(i) = norm (y .* exp (t) - 1, Inf);
 endfor

 ## Estimate order visually
 loglog (h, tol, "-ob",
         h, err, "-b",
         h, (h/h(end)) .^ 4 .* tol(end), "k--",
         h, (h/h(end)) .^ 5 .* tol(end), "k-");
 axis tight
 xlabel ("h");
 ylabel ("err(h)");
 title ("Convergence plot for ode45");
 legend ("imposed tolerance", "ode45 (relative) error",
         "order 4", "order 5", "location", "northwest");

 ## Estimate order numerically
 p = diff (log (err)) ./ diff (log (h))

Produces the following output

p =

  -0.0083500  -0.0358640   6.2262817   7.0685879   5.6481895   5.4964440   5.3061926   5.3054809

and the following figure

Figure 1

Package: octave